What he captures is that TIME is not a continum which becomes clear in my Cloud Cosmology which is embedded in a 3D manifold rather than a Space Time manifold which allows for TIME to be a continium.
He did generate one of the rare metrics while at it.
Gödel's Solution to Einstein's Field Equations
"Change becomes possible only through the lapse of time"
Jørgen Veisdal May 4
This is a free preview of a premium issue of the Cantor’s Paradise newsletter. If you enjoy it, consider supporting future such issues by signing up for a paid subscription at $5 per month. Thank you!
Einstein presenting the first Albert Einstein Award to Kurt Gödel and Julian Schwinger in 1951 (Photo: IAS Archive)
Following Kurt Gödel (1906-1978)’s publications on the first- and second incompleteness theorems (1931) and later work on Cantor’s continuum hypothesis (1947), Gödel in 1948 turned his attention to cosmology. In an extensive investigation of Einstein’s field equations, Gödel found one of few known exact solutions, whose implications—the “Gödel universe”—are very peculiar.
Gödel presented his solution to Einstein in the form of a manuscript on the occasion of the latter’s 70th birthday in 1949. Gödel was meant to have his manuscript ready for Paul Arthur Schlipp to include it in a book entitled Albert Einstein: Philosopher-Scientist* (Schlipp, 1949). Gödel, ever the perfectionist, however did not finish his essay until about a month before Einstein’s birthday and even then delayed sending it off for a while (Dawson, 2006). Notorious for his attention to detail, Gödel’s six-page manuscript eventually included 34 footnotes.
Group photograph from Einstein’s 70th birthday celebration at the Institute for Advanced Study. Present: Eugene Wigner, Hermann Weyl, Kurt Gödel, J. Robert Oppenheimer and others. (Photo: IAS Archive)
Gödel’s Interest in Physics
Gödel’s interest in physics is traceable back prior to his entry to the University of Vienna in 1924, age 18, where he was originally admitted to study theoretical physics. At the time, he had already read some of philosopher Immanuel Kant (1724-1804)’s work, and evaluated Goethe’s dispute with Newton, eventually siding with the latter (Wang, 1995). Historical documents indeed show Gödel on the 26th of January 1925 requesting Kant’s 1786 book on the foundations of natural science from the Library at the University of Vienna.
Fast forward 22 years, as he completed his work on ordinal definability and Cantor’s continuum hypothesis in 1947, by the following year Gödel’s interests were again gravitating towards the intersection of physics and philosophy. As Dawson (2006) intimately describes, the occasion for which Gödel would find himself solving Einstein’s notoriously difficult field equations begins with a request from Paul Arthur Schlipp, founder and editor of the book series Library of Living Philosophers. While visiting the Institute for Advanced Study in May of 1946, Schlipp invited Gödel to contribute a chapter for an upcoming volume of the series, on the philosophical implications of Einstein’s work. He did not propose a topic for Gödel, but likely assumed that Gödel (a close friend of Einstein) would write “something in the way of a personal tribute or memoir” (Dawson, 2006 p. 176).
Gödel had other plans. As Dawson notes, “their friendship had little to do with the topic Gödel ultimately chose to write about for Schlipp”. Indeed, as Einstein’s birthday approached, Gödel wrote his mother on February 26th 1949 still concerned about what to an actual gift might be:
“March 14 is Einstein’s seventieth birthday and I don’t know what I should give him. So far as I know him, he is not at all fond of such things. Adele knit for him a wool vest (handstitched things are very hard to get here), but then gave up the idea of giving it for the birthday and sent it to him in Florida instead. He wrote from there a charming note of thanks.“
At that point, Gödel had been working on the draft of his paper for over a year. An entry in the diary of Gödel’s close friend Oskar Morgenstern (1902-77) from a year prior (February 24th, 1948) notes that both he (Morgenstern) and Einstein were already then waiting for Gödel them to give them a copy of the “Kant-Einstein Aufsatz” (“Kant-Einstein Essay”). In correspondences with his mother, Gödel had at this point “for several weeks” been obsessed with the “problem” which, although he preferred to take breaks, would inevitably consume him (Dawson, 2006 p. 182). As he writes, even trying to listen to the radio or go to the movies (his favorite movie was supposedly ‘Show White and the Seven Dwarfs’), he would be able to do so with “only half an ear”.
Schlipp did eventually manage to get Gödel’s word that he would at least present Einstein with a copy of his manuscript at the planned gala birthday celebration, which he eventually did on March 19th 1949. In addition, as he wrote his mother on April 16th:
“After long searches I finally sent him an etching for his birthday”.
The final manuscript was next sent to Schlipp and published in the 7th volume of the series Library of Living Philosophers (Dawson, 2006) as:
Gödel, K. (1949a). ‘A Remark About the Relationship Between Relativity Theory and Idealistic Philosophy‘, in Schlipp, P.A. (ed) Albert Einstein: Philosopher-Scientist, pp. 555-563.
An extended version of the paper was later found in Gödel’s Nachlaß. Its reference is:
Gödel, K. (1946-49). ‘Some Observations about the Relationship between Theory of Relativity and Kantian Philosophy’. Manuscripts A,B and C. Unpublished.
The Gödel Universe
Gödel’s interest, as implied above, was in the relationship between Einstein’s relativity theory and the transcendental idealism doctrine advocated by Immanuel Kant. In his Critique of Pure Reason (1781), Kant outlines how space and time are pure forms of human intuition contributed by our own faculty or sensibility. Space and time, in Kant’s view, in other words do not have existence outside of experience, but are subjective forms of our sensibility and so an a priori condition rather than artefacts themselves. His interest in this aspect of Kant’s work had invoked Gödel’s curiosity as to “whether [the concept of absolute time] … is a necessary property of all possible cosmological solutions” of the field equations of general relativity (Dawson, 2006).
The first two pages of Gödel (1949a)’s six-page paper ‘A Remark About the Relationship Between Relativity Theory and Idealistic Philosophy’
The paper Gödel presented to Einstein, ‘A Remark About the Relationship Between Relativity Theory and Idealistic Philosophy’, is one of three philosophical essays published by Gödel in his lifetime. Remarkably accessible, even for layman, the paper includes discussions on:
The Nature of Time: A discussion of the nature of time itself, in relation to the works of Einstein and Immanuel Kant;
The Gödel Metric: Gödel’s proclamation of having discovered new solutions to Einstein’s field equations; and
Time Travel: A discussion of the implications of his solutions in relation to Einstein’s relativity theory;
Hao Wang (1921-95) summarizes the content of Gödel’s paper as follows (Wang, 1995):
The theory of relativity reveals that, in a systematic and precise organization of all our physical experience, it is by no means obvious that there is a unique natural linear ordering of all world-points or point-events.
In the first place, according to the special theory of relativity, each state of (uniform) motion determines a frame of reference and a temporal order. For two observers in different states of motion, the temporal orders are different, so that, for instance, it is possible to see A happening before B by one observer and B happening before A by the other.
Since we can envisage observers in very different states of motion, there are, relative to such observers, very different temporal orders. None of these temporal orders, however, can claim, without arbitrariness, the prerogative of being the natural or the real one, which is to represent the true universal lapse of time.
The Nature of Time
Gödel opens his essay by discussing the surprising insight relativity theory presents into the nature of time, “of that mysterious and seemingly self-contradictory being which, on the other hand, seems to form the basis of the world’s and our own existence”. In particular, Gödel points out, that the starting point of special relativity theory “consists in the discovery of a new and very astonishing property of time, namely the relativity of simultaneity”. By this Gödel is referring to Einstein’s discovery that, in relativity, the statement “A occurred before B” loses its objective meaning.
Only in 1976 did Gödel tell biographer Wang that his work on relativity theory had been inspired by his interest in Kant’s philosophy of space and time (as oppose to, the other way around, based on his frequent talks with Einstein). As he indeed notes in the 1949a paper, he had been particularly struck by the agreement “between Kant and relativistic physics insofar as in both theories the objective existence of a time in the Newtonian sense is denied”.
In Einstein’s general theory of relativity, the presence of the additional concept of matter helps eliminate the equal claims of different observers. That is, in all of the solutions to Einstein’s gravitational equations (before Gödel’s), ”the local times of all observers fit together in to one world time” (Gödel, 1949a p. 559):
“From this state of affairs, in view of the fact that some of the known cosmological solutions seem to represent our world correctly, James Jeans (1877-1946) has concluded that there is no reason to abandon the intuitive idea of an absolute time lapsing objectively”.
However, Gödel objects: “I do not think that the situation justifies this conclusion”. In particular, “[I] am basing my opinion chiefly on the following:”
“There exists cosmological solutions of another kind than those known at present”
Gödel’s is referring to his own (yet published) solutions to Einstein’s field equations, for which, as he notes “the […] procedure of defining and absolute time is not applicable, because the local times of […] special observers cannot be fitted together into one world time”. In a footnote, he notes that the most “conspicuous” property of his novel solutions (distinguishing them from those already known) is that the “compass of inertia in them everywhere rotates relative to matter, which in our world would mean that it rotates relative to the totality of galactic universes”.
The Gödel Metric
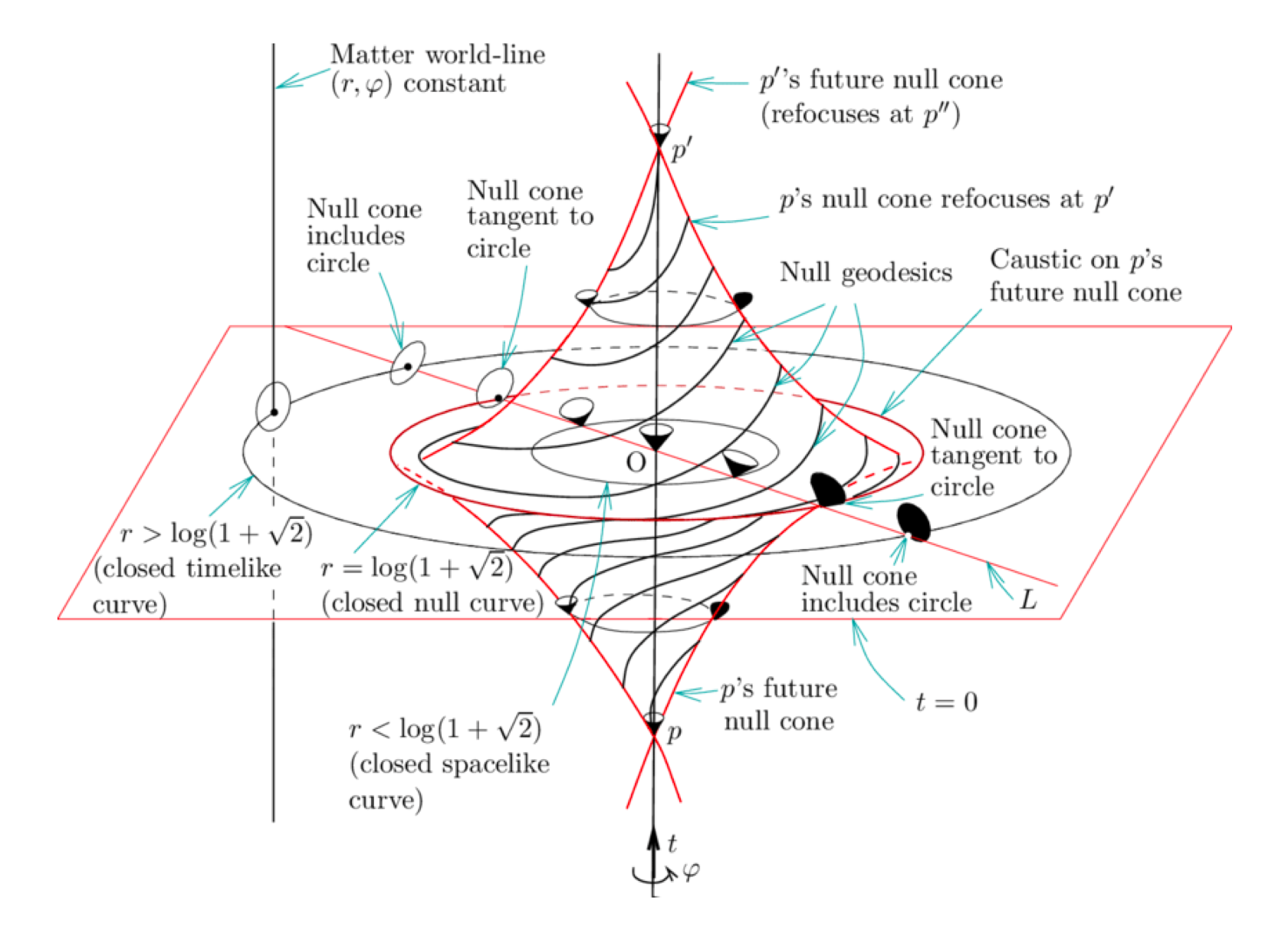
Spacetime Diagram of the Gödel Universe (Hawking & Ellis, 1973)
In a more technical 1952 paper on the same topic for the Proceedings of the International Congress of Mathematicians in Cambridge, Gödel wrote that “a directly observable necessary and sufficient criterion for the rotation of an expanding spatially homogeneous and finite universe” is that “for sufficiently great distances there must be more galaxies in one half of the sky than in the other half” (Dawson, 2006 p. 181). The more technical paper is:
Gödel, K. (1949b).An Example of a New Type of Cosmological Solutions of Einstein's Field Equations of Gravitation. Rev. Mod. Phys. 21, pp. 447-450.
The inference Gödel draws from his solutions are thus that, although they may not describe our universe, the “nonobjectivety of change” (nonexistence of absolute time) at least applies in some such universes (should they exist). Moreover, “it turns out that temporal conditions in these universes show other surprising features”, such as e.g. “making a round trip on a rocket ship in a sufficiently wide curve, it is possible in these worlds to travel back into any region of the past, present, and future, and back again, exactly as it is possible in other worlds to travel to distant parts of space”.
As Morgenstern later recorded in his diary:
“Talked a lot with Gödel. His cosmology is making good progress. Now you can in your universe travel back in time; respectively drive to any location in any short time. That will make a nice stir.”
Time Travel
"This state of affairs seems to imply and absurdity. For it enables one e.g., to travel into the near past of those places where he has himself lived. There he would find a person who would be himself at some earlier period of his life. Now he could do something to this person which, by his memory, he knows has not happened to him.”
Gödel is careful to make note that this observation, about time travel, is very much a technical observation rather than a prediction. He—for instance—quickly debunks any speculation that such travel would be physically feasible, writing “the velocities which would be necessary in order to complete the voyage in a reasonable length of time are far beyond everything that can be expected ever to become a practical possibility”. Somewhat sneakily, he however also makes use of this fact to argue for the viability of his universe, stating “therefore it cannot be excluded a priori, on the ground of the argument given, that the space-time structure of the real world is of the type described”.
To understand Gödel’s view better, again an entry from Morgenstern’s diary is illuminating. Towards the end of 1948, Morgenstern notes that neither of the models Gödel had obtained were in fact compatible with an expanding universe. Thus, Gödel’s was certainly aware that his rotating universe (as outlined in the 1949a essay) cannot be a model of our universe, with its observed red shift for stellar objects.
Gödel’s solutions did however demonstrate the possibility for the existence of such universes. Perhaps encouraged by this fact, he (Gödel) later expanded his investigation into the mathematical construction of a rotating expanding universe, which might be more compatible with observation. This investigation is summarized in the paper:
Gödel, K. (1952). Rotating Universes in General Relativity Theory. Proceedings of the International Congress of Mathematicians in Cambridge, Vol. 1. pp. 175-81.
In addition, two notebooks were later found in Gödel’s Nachlaß containing logs of observations of the angular orientation of galaxies—perhaps evidence of his hopes of finding physical clues which might help support future such constructions. As Dawson notes, Gödel at one point even inquired to physicist Freeman Dyson (1923-2020) about what the latest observational evidence for rotation were, which, much to Gödel’s dismay, Dyson informed him were non-existent.
Einstein’s Reaction
Gödel went on to lecture on his discoveries at the Institute for Advanced Study on May 7th, 1949. The talk was well attended. Gödel appears to have be in “good form” and spoke for an hour and a half, although as Morgenstern noted in his diary, few of Gödel’s colleagues seemed to be able to grasp the implications of his lecture. Indeed, as Dawson (2006) writes, most appear to have be astounded simply by the depth of his knowledge of physics.
In Einstein’s published remarks on Gödel’s essay, he heralds the work as “an important contribution”, noting that the possibility of closed time-like curves had “disturbed” him at the time of his development of the theory. Polite as ever, Einstein however also notes that it “might be interesting” to explore whether or not Gödel’s solutions could “be excluded on physical grounds”.
Einstein presenting the first Albert Einstein Award to Kurt Gödel and Julian Schwinger in 1951 (Photo: )
Although he did not “believe in” Gödel’s universe, in the weeks prior to his death six years later, Einstein did write—on the occasion of the death of his friend Michele Besso (Wang, 1995):
“So in quitting this world he has once again preceded me by a little. That doesn’t mean anything . For those of us who believe in physics, this separation between past, present, and future is only an illusion, however tenacious.”
For those interested in further exploring the implications of the Gödel universe, Brandeis University Professor of Philosophy Palle Yourgrau (1950-) later authored two books on the topic:
Yougrau, P. (1999). Gödel Meets Einstein: Time Travel in the Gödel Universe*. Open Court.
Yourgrau, P. (2006). A World Without Time: The Forgotten Legacy of Gödel and Einstein*. Basic Books.
Thank you for reading and subscribing to the Cantor’s Paradise newsletter. Please consider supporting future issues by becoming a paid subscriber, at $5 per month. You can unsubscribe at any time if you are dissatisfied.
Sincerely,
Jørgen
References
Dawson, J. (2006). Logical Dilemmas: The Life and Work of Kurt Gödel*. CRC Press.
Hawking, S.W. & Ellis, G.F.R. (1973). The Large Scale Structure of Space-Time*. Cambridge University Press.
Wang, H. (1995). Time in Philosophy and in Physics: From Kant to Einstein and Gödel. Synthese 102, pp. 215-234.
Wang, H. (1987). Reflections on Kurt Gödel*. Bradford Books.
* Amazon affiliate links




No comments:
Post a Comment