A framework to simulate the same physics using two different Hamiltonians

The Hamitonian generates the equations of motion.  This is actually not too surprising and undertstandable that no one tried to do this.  It could be really useful.

My work opens the door to setting up three and four axis problems that may be solvable.  Good lusck with that of course.  It involves setting up the Hamiltonians as the way forward.

So this starts to get really interesting.  Is it possible that consciousness is linked to the mathematics of Hamiltonians?  This provides a plausible mental framework.

A framework to simulate the same physics using two different Hamiltonians

by Ingrid Fadelli , Phys.org

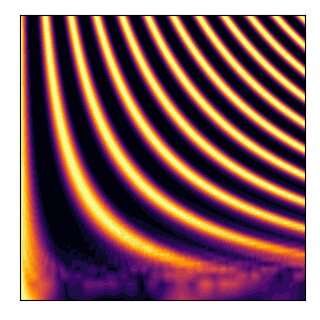
Fidelity between quantum states generated by the one-axis twisting Hamiltonian and the states generated by the Heisenberg XXX model with staggered field. Credit: Gietka et al.

https://phys.org/news/2021-06-framework-simulate-physics-hamiltonians.html?

Researchers at Okinawa Institute of Science and Technology Graduate University in Japan have recently been investigating situations in which two distinct Hamiltonians could be used to simulate the same physical phenomena. A Hamiltonian is a function or model used to describe a dynamic system, such as the motion of particles.

In a paper published in Physical Review Letters, the researchers introduced a framework that could prove useful for simulating the same physics with two distinct Hamiltonians. In addition, they provide an example of an analog simulation and show how one could build an alternative version of a digital quantum simulator.

"The idea came about when I was looking at the dynamical generation of entanglement in spin chains," Karol Gietka, one of the researchers who carried out the study, told Phys.org. "I noticed that the behavior of entanglement as a function of time in a certain model very much resembles entanglement behavior in the paradigmatic one-axis twisting model. Initially, I thought that one could map one system onto another one, but it was not possible as the Hamiltonians of the two systems were very different, which really confused me."

Gietka set out to rethink the principles of quantum simulators and then realized that in addition to the Hamiltonian, the initial state should also be taken into account as an ingredient of quantum simulators. Gietka and his colleagues defined a 'connector' operator and found that the same dynamics is observed from two different Hamiltonians if the initial state is an eigenstate of the connector.

This result indicates that using the same Hamiltonian is not always a necessary condition. As an example, they showed that the physics of one-axis twisting can be simulated by a spin chain with an external field, even though the one-axis twisting model has infinite range interactions and this spin chain model has only nearest-neighboring interactions. The Hamiltonian of these two models are physically different, i.e. having different energy spectra, but still one can simulate the one with the other if the dynamics starts with special states.

"The advantage of such an approach is that it relaxes the conditions imposed on the universal quantum simulator—-a quantum machine capable of simulating an arbitrary physical system," Gietka said. "One of its applications, which we present in our paper, is the creation of maximally entangled states of many-body systems exploiting only the interactions between the nearest elements of the system. Another application is an alternative version of the digital quantum simulator which might turn out to be less complex in certain cases than the original digital simulator."

Remarkably, the fact that a quantum simulator Hamiltonian can differ greatly from the Hamiltonian one wants to simulate could extend the scope of quantum simulation, as it means that one could create a simulator whose Hamiltonian does not agree with that of any systems existing in the world. These researchers' work could thus enable the design and realization of different types of quantum devices.

"I am now investigating how the idea of simulating the same physics with two distinct Hamiltonians can be harnessed to simulate physics of exotic quantum systems which seemingly should not exist," Gietka said. "I am also trying to figure out how one can use that idea in quantum metrology to collect precise measurements of unknown physical parameters."