The last chapter introduced us to the two equations used to calculate plasma fields. It is clear that they work in a step wise alternating fashion which is sufficient for a rough simulation. The problem is that we never achieve sufficient resolution. That is because any disturbance will produce spiral waves that bore down to impossible resolutions.
Thus we progress with developing empirical results and developing limited equations to predict behavior.
Here we discuss sheaths in particular and double layers. Right now we want an intuitive understanding of possibilities.
.
Essential Guide to the EU – Chapter 5 Plasma Sheaths, Cells, and Current-Free Double Layers
https://www.thunderbolts.info/wp/2011/12/03/essential-guide-to-the-eu-chapter-5/
The
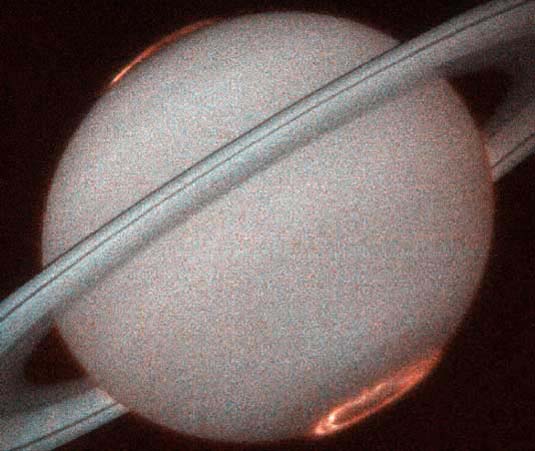
Saturn aurora’s reddish color is characteristic of ionized hydrogen
plasma. Powered by the Saturnian equivalent of (filamentary) Birkeland
currents, streams of charged particles from the interplanetary medium and
solar wind interact with the planet’s magnetic field and funnel down to
the polar regions. Double layers are associated with filamentary
currents and current sheets, and their electric fields accelerate ions
and electrons. Image credits: Wiki Commons; J.Trauger (JPL), NASA,
Hubble Space Telescope
5.1 Plasma Temperature and Potential
We have seen that temperature is a
measure of the thermal energy of the particles in matter. More
specifically, temperature is a measure of the kinetic energy of the
particles’ random thermal motion.
An electron has only 1/1840th the mass
(approximately) of a proton, so electrons will have much higher
velocities than ions at the same temperature. This is because kinetic
energy is proportional to the mass of the particle and the square of its
velocity, K.E. = 1/2 mv². Therefore, at the same temperature, the
ratio of velocities will be inversely proportional to the square root of
the particle masses.
For example, average electron velocity will be around 43 (i.e.,
√1840) times higher than the velocity of a single proton. If the
positive ions in the plasma are heavier than a single proton then the
difference will increase accordingly.
What is more, because of the Principle of Conservation of Momentum, an electron will tend to undergo a larger change in its velocity than an ion does in a collision between the two particles.
The electrons’ higher velocity results
in more rapid interactions, which means that the electrons reach
thermodynamic equilibrium (“the same temperature”) amongst themselves
much faster than the ions do. Any increase in velocity, whether from
collisions or external energy inputs, is therefore ‘shared out’ amongst
the electrons very rapidly.
For these reasons, it is common for the
electron temperature in a plasma to be different from the ion
temperature. Often the electron temperature will be higher than the ion
or the ambient temperatures. This is especially common in weakly ionized
plasmas, where the ions are often near the ambient temperature while
the faster-moving electrons have high temperatures. Wikipedia reference
on plasma temperature here.
In a plasma the temperature is often
expressed as a thermal potential which is equal to the potential drop
(change in voltage) through which the particles would have to fall in
order to gain the same amount of energy. The kinetic energy can then be
expressed in electron-volts or eV.
The hotter the plasma, the faster the
electrons and ions are moving in random thermal motion and the higher
their potential. A potential of 1 eV is equivalent to a temperature of
11,604.5 K. Particles with potentials many orders of magnitude higher
are common in space.
Note:
one must be cautious about the conversion between electron volts and
thermal temperatures in plasma. Plasmas can become ordered so that
charged particles follow paths that are aligned with the local direction
of the accompanying magnetic field. Such current flows are termed field-aligned currents.
Under this condition, charged particles are moving approximately
parallel to one another, and, partly due to the low density of
particles, collisions of the thermal variety can become very rare.
The
high temperature alleged for the solar corona is based on spectroscopic
observations of the light (electromagnetic radiation including
frequencies outside visible light) which indicate how much ionization of
atoms has occurred. The ionization energy in eV is inferred from the
wavelengths of light emitted, and converted by the formula above
to equivalent temperature.
The thermal aspect of temperature which is caused by large numbers of random collisions is not necessarily present, however, even if there has been sufficient energy input to strip electrons away from their nuclei. The electrons can be fast (energetic) while their (thermal) collision rates are low.
The thermal aspect of temperature which is caused by large numbers of random collisions is not necessarily present, however, even if there has been sufficient energy input to strip electrons away from their nuclei. The electrons can be fast (energetic) while their (thermal) collision rates are low.
The high velocity of the electrons is
especially important in understanding many aspects of plasma behavior,
including radio galaxies, galactic and stellar jets, and production of
synchrotron radiation and cosmic rays.
5.2 Development of Surface Sheaths
If plasma is contained within a
laboratory tube or other vessel, the electrons and ions in the plasma
will impact the walls of the vessel with a frequency proportional to
their velocity. On impact, particles are absorbed by the walls.
As the electrons have much higher velocities than the ions, the rate
of electron impact will be many times that of the ion impacts. As a
result, the walls of the vessel will acquire a negative charge.
As the negative charge on a surface
develops, arriving electrons will tend to be repelled from the surface.
Only those electrons with sufficient velocity to overcome the repulsion
will still be able to impact the surface. The negative charge on the
surface will continue to increase until the number of electrons hitting
the surface equals the number of positive ions arriving. The plasma and
the surface will have achieved a balance, or steady state.
In the steady state, only the fastest
electrons will still be able to get through the adverse potential
gradient from the negative surface. Most electrons will be prevented
from approaching the surface. This results in a layer of plasma adjacent
to the surface in which the ions outnumber the electrons. This positive
layer is known as a Debye Sheath.
Similar effects are found if the
surface is charged negatively or positively by connecting a source of
potential such as a battery. The charge on the surface repels like
charges in the plasma, leaving behind an oppositely-charged sheath.
5.3 Extent of a Sheath
A surface sheath does not have a
definite physical boundary but may be considered to end where the
potential resulting from the negative surface and the positive sheath
acting together balances the potential of the plasma itself. In other
words, the sheath boundary is where the potential is just sufficient to
repel electrons with energy equal to the plasma potential.
For example, if the plasma potential is
+1V then the nominal boundary will have a potential of -1V. The
explanation is as follows: The boundary has a negative potential because
the sheath must repel approaching electrons. The electrons in the
plasma have a kinetic energy of 1eV. Therefore, the sheath needs -1V
potential to stop the approaching electrons from reaching the surface.
This is analogous to rolling a ball up a
hill. If the ball has enough kinetic energy then it will reach the top.
If not, it will get a part of the way up before coming to a stop and
then rolling down again.
The sheath potential is analogous to the height of the hill.
The sheath potential is analogous to the height of the hill.
It can be seen that the sheath does not
have a ‘hard’ edge and in fact the potential field arising from the
negative surface continues past the sheath ‘boundary’. Nevertheless, the
boundary may be taken as the point at which the negative surface is
effectively ‘neutralized’ by the sheath because electrons with the
plasma potential are ‘reflected’ back into the plasma at that point.
American chemist and Nobel laureate
Irving Langmuir developed measurement methods and observations of plasma
actions. An interesting and useful PDF lecture, Plasma, Sheaths and Surfaces — The Discharge Science of Irving Langmuir, can be found here.
5.4 Charged Bodies in a Plasma
Similar sheaths will form around any
charged body in a plasma where the body has a different potential from
the plasma itself. The plasma effectively isolates the foreign body by
forming a sheath round it. The sheath will tend to screen out the
electrostatic field from the alien charge in the same way that a sheath
tends to isolate a negatively charged surface. The body eventually may
be neutralized by opposite charges that it absorbs.
If the charged body can artificially be
given a positive or negative charge by connecting it to an external
source such as a battery, ions or electrons, depending on the charge,
will be attracted to the body and so a current will flow. By careful
measurement of the current for a range of voltages, it is possible to
measure the potential of the plasma itself. One such device is named a
Langmuir Probe after Irving Langmuir, 1881–1957.
Current flow from the solar wind can be
observed at planets with magnetic fields which have polar “cusps” or
“holes” that guide charged particles down to and through the body,
creating auroral displays in the upper atmosphere.
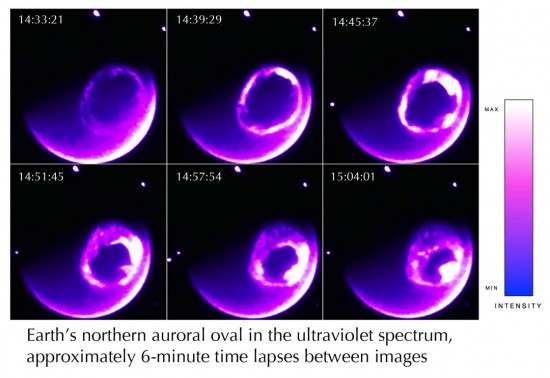
Half-hour time lapse evolution of Earth’s auroral oval, seen in this NASA image in ultraviolet light (false color)
At smaller scales, some planetary moons
move in plasma-filled orbits, with charged particle flows directed from
the moons’ polar regions along magnetic field lines to and from
“hotspots” in the auroral ovals of the larger planet. Examples include
Ganymede, Europa and Io at Jupiter, Enceladus at Saturn, and possibly
Uranus and Neptune as well.

Io-Jupiter field aligned polar current or “flux tubes”, creating not volcanoes, but enormous, long-lasting electrical discharges which machine away Io’s surface and deposit it as ions and compounds in its plasma torus. Credit: Nasa/Cassini Imaging Team

Saturn and its polar electrical connections to Enceladus. Measured cross section of current tube, above; Enceladus south pole jets where current is machining away the icy surface and depositing it into Enceladus ionosphere and plasma torus, similar to Io, above. NASA/Cassini Imaging team
5.5 Cellularization in Plasma
Similar effects also occur between two
adjacent regions of plasma with different characteristics. For example,
the two regions may have different temperatures, densities, or degrees
of ionization. In this situation, the different velocity distributions
in the two regions will set up a double sheath at the boundary whereby
each region effectively insulates itself from the other.
The double sheath will consist of
adjacent thin layers of positive and negative charge, separated by a
relatively small distance. It is one type of Double Layer. Because no
externally driven currents are involved, sheaths between different
plasma regions are known as Current-Free Double Layers (CFDL). More on
double layers in plasma here.
Note especially the external links, linked reference papers and
publications at the bottom of this article. Double layers and sheaths
are well-known phenomena in plasma dynamics, described in textbooks and
best described in Wiki’s discussion of the Vlasov-Poisson equation:
“In general the plasma distributions near a double layer are necessarily strongly non-Maxwellian¹, and therefore inaccessible to fluid models.
In order to analyze double layers in full generality, the plasma must
be described using the particle distribution function, which describes
the number of particles of species α having approximately the velocity v near the place x and time t”
¹[From Wikipedia, Physical Applications of Maxwell-Boltzman Distributions: The Maxwell–Boltzmann distribution applies to ideal gases close to thermodynamic equilibrium with negligible quantum effects and at non-relativistic speeds.
It forms the basis of the kinetic theory of gases, which explains many
fundamental gas properties, including pressure and diffusion.] (Emphasis
by Editor)
Importance of the reference above: This is the reason that conventional hydrodynamic and magnetohydrodynamic equations of fluid
flow are inadequate to a full and reasonably accurate mathematical
description of plasma dynamics. Consequently the computational method
called particle-in-cell (PIC) simulation was developed for plasma
modeling in massively parallel computer systems in the 1980s. Here is a Wikipedia article on PIC, and here is a more technical paper on the subject.
5.6 Formation of a Current-Free Double Layer (CFDL)
We have seen that CFDLs form between
regions of plasma with different characteristics. As an example, let us
consider the effect of a temperature difference (in electron volts, ref.
5.1 above).
This causes an electric field to build
up, which will accelerate electrons back to the hotter region. A net
flow of electrons to the cold region will continue to build up the
electric field until a balance is achieved between the numbers of hotter
electrons moving to the cool region and the number of electrons being
accelerated back to the hot region by the electric field.
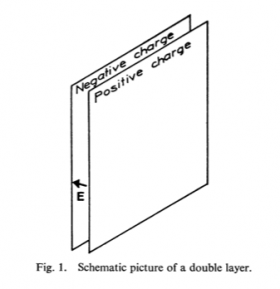
Credit: Double layer image from “A Double-Layer Review”, Lars P. Block, Swedish Royal Institute , Stockholm; Astrophysics & Space Science, July, 1977
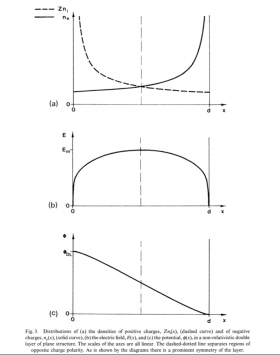
Credit: “On the Physics of Relativistic Double Layers”, Per Carlqvist, Dept. of Plasma Physics, Royal Institute of Technology, Stockholm; Astro
The thin regions near the boundary
containing an excess of ions or electrons constitute a Double Layer at
the boundary which has an electric field and associated potential drop
across it.
The formation of sheaths at boundaries
between different plasma regions creates cells of plasma. This
cellularization is a defining characteristic of plasma behavior. Gases do not behave in this fashion, which is one reason why it is not possible to apply gas laws to plasmas.
5.7 Similarity to Fluid Mechanics
At first sight, a Double Layer (DL)
appears to be something like a shock wave in fluid dynamics. Indeed, a
DL does share some characteristics of a shock wave in that it separates
regions of differing characteristics and acts to accelerate the medium.
In the case of DLs, however, the acceleration occurs as a result of the strong electric field set up between the oppositely charged layers.
As the force from the electric field depends on the charge on the
particle, ions and electrons are accelerated in opposite directions.
Neutral particles are not accelerated at all by the electric field, but
may be entrained through viscous or other effects.
Note that the formation of Double Layers cannot be effectively modeled by fluid analyses such as magneto-hydrodynamics (MHD) because it is caused by and is dependent on motions of different individual particles, not on the bulk motion of the plasma.
Double layers are one of the most important aspects of the self-organizing characteristics of cosmic plasma, as we will see.
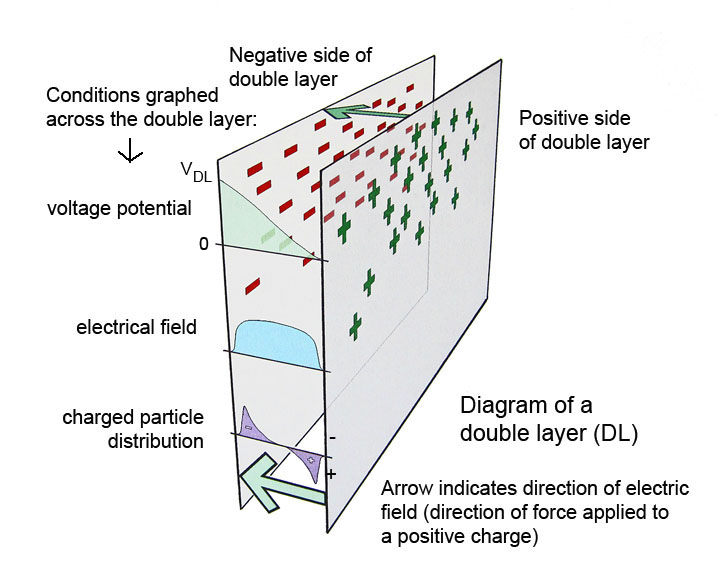
Image adapted from above sources to illustrate charge relationships and electric field potential in a DL – J. Johnson, 2011
A general introduction to Plasma Physics from Wikipedia’s perspective can be found here ,
including properties, phenomena and mathematical models. While
Wikipedia often has well-written articles, like anything else it can
sometimes be unreliable or incomplete, or prone to biased editing, so always use care when evaluating articles from Wiki, as well as other sources
End of Chapter 5
No comments:
Post a Comment