This is meant as a handy refresher only and may help to check out notation. This is not meant to help those unfamiliar with the topics. We also lost a couple of paragraphs due to format forces brought about by attempts to convert to code.
Otherwise this is meant for the record.
Appendix I – Vector Algebra
Vector algebra is formulated to handle vectors; i.e., quantities with both magnitude and direction. Normal algebra, geometry and trigonometry are efficient at dealing with scalar
quantities, that is, those with only magnitude, but are inefficient at
handling vectors. Vector algebra is an efficient way of solving 2D and
3D problems involving vectors without the need for cumbersome geometry.
The electro-magnetic (e/m) field is a vector field of forces acting
on charged objects. As forces are vector quantities (forces acting in an
associated direction), the e/m field equations involve vectors.
Vector algebra can be formulated for Cartesian, cylindrical and
spherical coordinates. Appropriate choice of coordinate system for
cylindrically or spherically symmetric problems avoids needless
complexity arising from the use of an inappropriate coordinate system
and will also clearly show the symmetry of the solution.
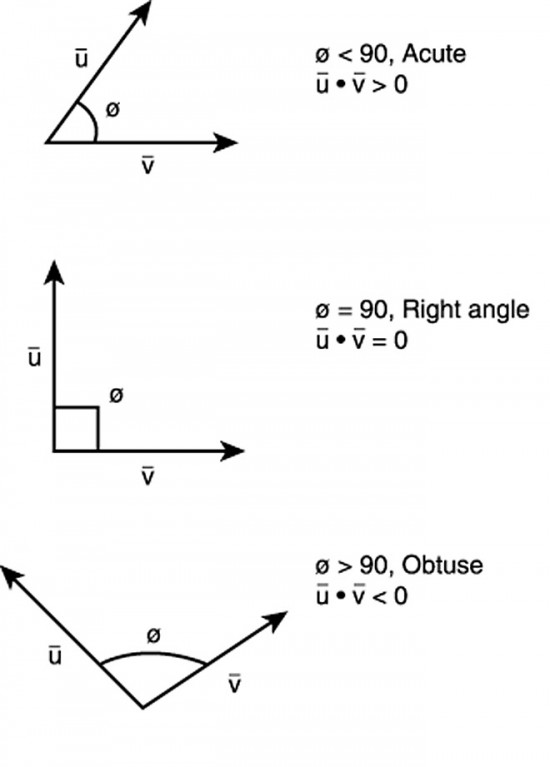
Two important results of vector algebra involve multiplication of vectors. Vectors will be indicated by bold text.
Paragraph trashed here
The cross product A×B (read as “A cross B”) is defined as AB sin(θ)an, where an is the unit vector normal to the plane of A and B.
Note that the cross product of two vectors is also a vector and its
direction is orthogonal (perpendicular) to both A and B; i.e., the
resultant vector involves a third dimension compared to the 2D plane
containing the first two vectors.
Vector algebra defines another important operator, Del,
or Δ. Del is analogous to the differential operator D in calculus where
D represents the operation d/dx. Two further results using Del are
important in analyzing e/m fields.
Paragraph trashed here.
source of the electric flux, that is the positive point charge; therefore the
divergence of the electric flux density vector field over that surface
will be positive, and equal to the enclosed charge. This is Gauss’ Law.
(see Appendix II, e/m field equations)
Note that Div A involves a dot product and is
therefore dependent on angles. The angle is usually that between the
vector and the normal to the surface being analyzed.
Δ×A or Curl A is the curl of the vector field A. The curl of a vector field is another vector field which describes the rotation of the first vector field; the magnitude of Δ×A is the magnitude of the rotation, and the direction of Δ×A
is the axis of that rotation as determined by the right-hand rule. If
one imagines any 3D vector field to represent fluid flow velocities,
then the curl of the field at a point would be indicated by the way a
small sphere or a paddlewheel placed at that point would be rotated by
the flow. In a 2D flow it is easy to see that the direction of the axis
of rotation of a circle (the 2d analogue of a sphere) in the flow will
be in the third dimension, as is given by the use of the cross product
in calculating the curl.
Additionally, the Del operator can be applied to a scalar field V. ΔV or Grad V is a vector field defining the gradient
of the scalar function V. ΔV lies in the direction of the maximum
increase of the function V. If applied to a potential function, then
Grad V is a vector field that is everywhere normal to the equipotential
surfaces.
Two useful properties of the Curl operator are:
(1) the divergence of the curl of any vector field is the zero scalar; i.e., Δ・(Δ×A) = 0
(2) the curl of a gradient of any vector field is the zero vector; i.e. Δ×(Δf) = 0 for any scalar function f dependent on position, as in f(x,y,z)
Example:
To visualize (2), think of a scalar field such as an area of hilly land,
where contours of constant elevation above sea level are “drawn” along
the ground. Elevation “h” at any given point (x,y,z) would then vary
with position, so its function is h(x,y,z). The gradient del(h) would
be a vector that points, starting at the point (x,y,z), perpendicular to
the contour line through (x,y,z) and straight “down the hill”. Imagine
the way water flows downhill, or which way a marble would roll, and
that’s the direction the gradient vectors point, always perpendicular to
the equal-elevation contour at any point. Because these vectors are
straight, they have no curl, or bend. That’s why, mathematically, ‘del × (del h) = 0′.
In practice, this means that an electric field in which the lines of flux are straight (e.g.,
between the layers of a plasma double layer or a capacitor, ignoring
edge effects where the lines are not straight), a charged particle will
be accelerated from rest in a straight line: the electric field has no
curl.
Vector algebra becomes even more important in analyzing particle
interactions when several forces may be present, as when a charged
particle enters both an electric field and an associated magnetic field
simultaneously, at an oblique angle so that its motion vector can have
one component normal to the field lines and another (“drift”) parallel
to them. The Mathematica©-based images in Chapter 4, ¶4.3, are
indicative of some of the complexities of such interactions using only 1
particle. Plasma are double digit orders of number of particles higher
than this simplest case, and the feedback mechanisms and complex
particle motions that develop cause the plasma to create and maintain
charge separation, to separate bodies with one electrical field
potential from a volume of differente potential, to initiate current
flows, to accelerate particles to relativistic velocities and radiate
strongly, to pinch and roll up current sheets into filamentary
conducting plasma structures like lightning, coronal loops and galactic
jets.
###
TRACE imagery of current loop arcades and prominences above an active region on the Sun
Appendix II: The Electro-magnetic Field Equations
https://www.thunderbolts.info/wp/2012/06/20/appendix-ii-the-electro-magnetic-field-equations/
Maxwell’s Equations and the Lorentz Force Law together comprise the e/m field equations; i.e., those equations determining the interactions of charged particles in the vicinity of electric and magnetic fields and the resultant effect of those interactions on the values of the e/m field.
For ease of explanation, the following will refer to “fields” as though they possess some independent physical reality. They do not. The use of fields is as an aid in understanding how forces exerted by and upon real particles, and how the positions (coordinates) of those particles may exist at a given time, or may vary over an interval of time. Field lines are also convenient notational devices to aid in understanding what physically is going on, and are not “real”. An oft-used example is the set of lines or contours of equal elevation relative to some fixed reference value, often found on topographic maps of land areas, and varying pressure distributions on weather charts. Such lines do not exist as real physical entities; they can be used for calculation and visualization of simple or complex phenomena, but they do not effect changes or position or exert force or anything else, themselves. Imagining that they are real is called reification; it can be a convenient aid to better understanding, but it is incorrect to say that field lines of any type are real or “do” anything.
The implications of Maxwell’s Equations and the underlying research are:
- A static electric field can exist in the absence of a magnetic field; e.g., a capacitor with a static charge Q has an electric field without a magnetic field.
- A constant magnetic field can exist without an electric field; e.g., a conductor with constant current I has a magnetic field without an electric field.
- Where electric fields are time-variable, a non-zero magnetic field must exist.
- Where magnetic fields are time-variable, a non-zero electric field must exist.
- Magnetic fields can be generated in two ways other than by permanent magnets: by an electric current, or by a changing electric field.
- Magnetic monopoles cannot exist; all lines of magnetic flux are closed loops.
The Lorentz Force Law expresses the total force on a charged particle exposed to both electric and magnetic fields. The resultant force dictates the motion of the charged particle by Newtonian mechanics.
F = Q(E + U×B) (remember, vectors are given in bold text)
where F is the Lorentz force on the particle; Q is the charge on the particle; E is the electric field intensity (and direction); and B is the magnetic flux density and direction.
Note that the force due to the electric field is constant and in the direction of E, so will cause constant acceleration in the direction of E. However, the force due to the combination of the particle’s velocity and the magnetic field is orthogonal to the plane of U and B due to the cross product of the two vectors in vector algebra (Appendix I). The magnetic field will therefore cause the particle to move in a circle (to gyrate) in a plane perpendicular to the magnetic field.
If B and E are parallel (as in a field-aligned current situation) then a charged particle approaching radially toward the direction of the fields will be constrained to move in a helical path aligned with the direction of the fields; that is to say, the particle will spiral around the magnetic field lines as a result of the Lorentz force, accelerating in the direction of the E field.
Further Discussion of Maxwell’s Equations
The Maxwell Equations are the result of combining the experimental results of various electric pioneers into a consistent mathematical formulation, whose names the individual equations still retain. They are expressed in terms of vector algebra and may appear, with equal validity, in either the point (differential) form or the integral form.
The Maxwell Equations can be expressed as a General Set, applicable to all situations; and as a “Free Space” set, a special case applicable only where there are no charges and no conduction currents. The General Set is the one which applies to plasma:

where
- E is the electric field intensity vector in newtons/coulomb (N/C) or volts/meter (V/m)
- D is the electric flux density in C/m2; D = εE for an isotropic medium of permittivity ε
- H is the magnetic field strength and direction in amperes/meter (A/m)
- B is the magnetic flux density in A/N・m, or tesla (T); B = μH for an isotropic medium of permeability μ
- Jc is the conduction current density in A/m2; Jc = σE for a medium of conductivity σ
- ρ is the charge density, C/m3
By definition, electric flux ψ originates on a positive charge and terminates on a negative charge. In the absence of a negative charge flux “terminates at infinity”. If more flux flows out of a region than flows into it, then the region must contain a source of flux; i.e., a net positive charge.
Gauss’ Law equates the total (net) flux flowing out through the closed surface of a 3D region (i.e., a surface which fully encases the region) to the net positive charge within the volume enclosed by the surface. A net flow into a closed surface indicates a net negative charge within it.
Note that it does not matter what size the enclosing surface is – the total flux will be the same if the enclosed charge is the same. A given quantity of flux emanates from a unit of charge and will terminate at infinity in the absence of a negative charge. In the case of an isolated single positive charge, any sphere, for example, drawn around the charge will receive the same total amount of flux. The flux density D will reduce in proportion (decrease per unit area) as the area of the sphere increases.
Gauss’ Law for Magnetism states that “the total magnetic flux out of a closed surface is zero”.
Unlike electric flux which originates and terminates on charges, the lines of magnetic flux are closed curves with no starting point or termination point. This is a consequence of the definition of magnetic field strength, H, as resulting from a current (see Ampere’s Law, below), and the definition of the force field associated with H as the magnetic flux density B = μH in teslas (T) or newtons per amp meter (N/Am).
Therefore all magnetic flux lines entering a region via a closed surface must leave the region elsewhere on the same surface. A region cannot have any sources or sinks. This is equivalent to stating that magnetic monopoles do not exist.
Ampere’s Law with Maxwell’s Correction
Ampere’s Law is based on the Biot-Savart Law
dH = (I dl×ar) / 4πR2
which states that “a differential (i.e., tiny segment of) magnetic field strength dH at any point results from a differential current element I dl of a closed current path of current I). The magnetic field strength varies inversely with the square of the distance R from the current element and has a direction given by the cross-product of I dl and the unit vector ar of the line joining the current element to the point in question. The magnetic field strength is also independent of the medium in which it is measured.
As current elements have no independent existence, all elements making up the complete current path, i.e., a closed path, must be summed to find the total value of the magnetic field strength at any point. Thus:
H = ∫ (I dl×ar) / 4πR2
where the integral is a closed line integral which may close at infinity.
Thence, for example, an infinitely long straight filamentary current I (closing at infinity) will produce a concentric cylindrical magnetic field circling the current in accordance with the right-hand rule, with strength decreasing with the radial distance r from the wire, or:
H = (I/2πr) ar
(note the vector notation in cylindrical coordinates; the direction of H is everywhere tangential to the circle of radius r)
Ampere’s Law effectively inverts the Biot-Savart Law and states that “the line integral of the tangential component of the magnetic field strength around a closed path is equal to the current enclosed by the path”, or
∫H・dl = Ienc where the integral is a closed line integral
Alternatively, by definition of curl, Curl H or Δ×H = J, the current density.
This effectively means that a magnetic field will be generated by an electric current.
However, this only applies to time-invariant currents and static magnetic fields. As Jc = σE, this implies that the electric field is constant as well.
To overcome these restraints so as to allow for time-varying charge density and to allow for the correct interpretation of the propagation of e/m waves, Maxwell introduced a second term based on the Displacement Current, JD, where
JD = δD/δt
arising from the rate of change of the electric field E.
Maxwell’s correction, as included in the revised Law, dictates that a magnetic field will also arise due to a changing electric field.
Faraday’s Law states that “if the magnetic flux Φ, linking (i.e., looping through) an open surface S bounded by a closed curve C, varies with time then a voltage v around C exists”; specifically
v = -dΦ/dt
or, in integral form,
∫cE・dl = -d(∫s B・dS)/dt for a plane area S and B normal to S
Thus if B varies with time there must be a non-zero E present, or, a changing magnetic field generates an electric field.
The minus sign in the equation above indicates Lenz’s Law, namely “the voltage induced by a changing flux has a polarity such that the current established in a closed path gives rise to a flux which opposes the change in flux”.
In the special case of a conductor moving through a time-invariant magnetic field, the induced polarity is such that the conductor experiences magnetic forces which oppose its motion.

No comments:
Post a Comment